寻找二叉查找树中的下一个结点
一,问题描述
给定一棵二叉查找树,以及某个结点的值。查找该结点的下一个结点。如果该结点是最大的,则返回 null
对于二叉查找树而言,它是中序遍历有序的。某结点的下一个结点 就是:中序遍历输出的下一个结点。
二,问题分析
假设需要查找 node 结点的下一个结点,需要考虑三种情况:
①node 节点有右孩子
下一个结点就是以node结点的右孩子为根的子树中的最左下结点。如下图:node=8,它的下一个结点为12.

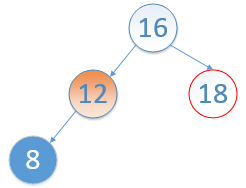
②node 节点没有右孩子时,node节点是其父结点的左孩子。如下图,结点8的下一个结点是结点12
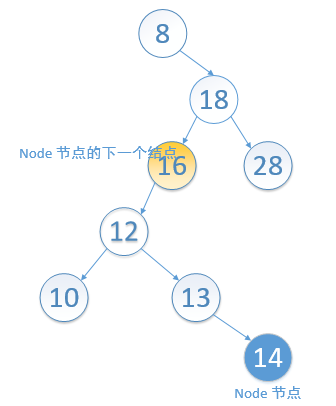
③node 节点没有右孩子时,node节点是其父结点的右孩子,如下图,结点14 的下一个结点是 结点16
如何在一棵二叉树中查找某个结点?
可以用先序遍历的思路。但是一定要注意递归的实现---第11行的 return target 是很有意义的。
在每一次的递归调用中,每个方法都有一个自己的 target 局部变量。如果在这个方法里面找到了目标结点,如果没有 return 返回的话,当递归回退时就会丢失“已找到的目标结点”----即上一层的 find 方法中的target 变量还是null(尽管在下一层递归中已经找到了目标结点)
通过第11行的 return 语句,如果在某一层还未找到目标结点,则会继续递归调用下去,如果找到了,在 return 的时候,上一层的find方法的target变量就不会为 null , 从而在最终 find 方法结束时,返回找到的目标结点。
1 //采用先序遍历查找值为ele的结点 2 private BinaryNode find(BinaryNode root, int ele){ 3 if(root == null) 4 return null; 5 if(root.ele == ele) 6 return root; 7 BinaryNode target = null; 8 target = find(root.left, ele); 9 if(target == null)//如果左子树中没有值为ele的结点,if成立,在右子树中查找 10 target = find(root.right, ele); 11 return target; 12 }
①第3-4行是应对查找到叶子结点的情况
②第5-6行,是成功查找到了指定结点的情况。(①②类似于先序遍历中的访问根结点)
③第8行,表示先在左子树中查找(类似于先序遍历左子树)
④第9-10行if表示在左子树中未查找到该结点,则查找右子树⑤第11行,返回查找的结点。若返回null,表示未找到
三,代码分析
①node 节点有右孩子
1 if(node.right != null) 2 { 3 BinaryNode current = node.right; 4 while(current.left != null) 5 { 6 current = current.left; 7 } 8 nextNode = current; 9 }
第3行,先定位到node结点的右孩子。
第4行while循环,查找最左下结点
②node 节点没有右孩子时,node节点是其父结点的左孩子
1 else if(node.parent != null){//node结点 是 parent 的孩子 2 if(node.parent.left != null && node.parent.left.equals(node))// node 是 parent 的左孩子 3 nextNode = node.parent;
如果node节点是其父结点的左孩子,那么下一个结点就是node节点的父结点。
③node 节点没有右孩子时,node节点是其父结点的右孩子
1 else{//node 是 parent的右孩子 2 BinaryNode current = node.parent; 3 //一直往着右孩子的父结点指针向上走 4 while(current.parent.right != null && current.parent.right.equals(current)) 5 { 6 current = current.parent; 7 } 8 nextNode = current.parent; 9 }
要注意第4行while循环中的第一个条件:current.parent.right != null
为什么不要判断 current.parent != null 呢?因为在前面的if语句中已经判断了(if(node.parent != null)
四,完整代码实现

public class BSTNextNode { private class BinaryNode{ int ele; BinaryNode left; BinaryNode right; BinaryNode parent; int hash;//cache hashCode public BinaryNode(int ele) { this.ele = ele; parent = left = right = null; } @Override public boolean equals(Object obj) { if(obj == null) return false; if(!(obj instanceof BinaryNode)) return false; BinaryNode node = (BinaryNode)obj; return node.ele == this.ele; } @Override public int hashCode() {// 参考《effective java》中覆盖equals方法 int result = hash; if(result == 0){ result = 17; result = result*31 + ele; hash = result; } return result; } @Override public String toString() { return ele + " "; } } private BinaryNode root; public void buildTree(int[] eles){ if(eles == null || eles.length == 0) return; for (int ele : eles) { insert(ele); } } private void insert(int ele){ root = insert(root, ele); root.parent = null; } private BinaryNode insert(BinaryNode root, int ele){ if(root == null) return new BinaryNode(ele); if(root.ele > ele){ root.left = insert(root.left, ele); root.left.parent = root; }else{ root.right = insert(root.right, ele); root.right.parent = root; } return root; } //寻找值为ele的那个结点的 下一个结点 public BinaryNode nextNode(int ele){ BinaryNode node = find(ele);//找到Node值为ele的结点在BST中的位置 if(node == null) throw new IllegalArgumentException(ele + " not in tree"); BinaryNode nextNode = null; if(node.right != null) { BinaryNode current = node.right; while(current.left != null) { current = current.left; } nextNode = current; }else if(node.parent != null){//node结点 是 parent 的孩子 if(node.parent.left != null && node.parent.left.equals(node))// node 是 parent 的左孩子 nextNode = node.parent; else{//node 是 parent的右孩子 BinaryNode current = node.parent; //一直往着右孩子的父结点指针向上走 while(current.parent.right != null && current.parent.right.equals(current)) { current = current.parent; } nextNode = current.parent; } }else{//node 没有父结点.那它就是BST中的最大的结点---此时它的下一个结点视为null // nextNode = node; ; } return nextNode; } //查找二叉树中值为ele的结点,并返回该结点 private BinaryNode find(int ele){ if(root == null) throw new IllegalStateException("bst is null"); return find(root, ele); } //采用先序遍历查找值为ele的结点 private BinaryNode find(BinaryNode root, int ele){ if(root == null) return null; if(root.ele == ele) return root; BinaryNode target = null; target = find(root.left, ele); if(target == null)//如果左子树中没有值为ele的结点,if成立,在右子树中查找 target = find(root.right, ele); return target; } //hapjin test public static void main(String[] args) { // int[] eles = {20,10,30,15,18,26,22,8,40}; int ele = 20; int[] eles = {20,10,15}; BSTNextNode bstTree = new BSTNextNode(); bstTree.buildTree(eles);//构造一棵二叉树查找树 BinaryNode next = bstTree.nextNode(ele);//查找值为ele结点的下一个结点 System.out.println(next); } }
五,参考资料




 浙公网安备 33010602011771号
浙公网安备 33010602011771号